计算机电路基础
根据教材制作讲稿
2006.8.
目录
1.1 电路的组成及电路分析的概念(P1)
电路分析:已知电路结构及参数,求出电路中的电量参数。
电路设计:已知输入输出的要求,设计电路结构及参数。
电路组成(P2)
直流电压源、直流电流源、支路、
节点(多支路连接点)、回路(闭合路径)。
1.2 电路中的主要物理量及参考方向
1.2.1 电流及参考方向(P3)
假定电流参考方向,电流真实方向由“+”“-”确定。
| a○---□---○b
i-----→ |
1.2.2 电压及参考极性(P4)
1.电压差、电压降、电压极性、参考节点、电位、参考极性。
| A○--+□---○B | A○---□---○B
u=2V-----→ |
2.关联参考方向:电压的参考极性与电流的参考方向相同。(P6)
非关联参考方向:电压的参考极性与电流的参考方向不同。
| A○--+□---○B
u=3V-----→ i=2A-----→ |
A○--+□---○B
u=3V-----→ i=2A←----- |
1.2.3 功率(P6)
图1.2.6 电路(a)(b)中,u,i 取关联参考方向
u=3V,i=5A,吸收功率 p=u·i=3×5=15W
图1.2.6 电路(c)(d)中,u,i 取非关联参考方向
u=-2V,i=-3A,吸收功率 p=-u·i=-(-2)x(-3)=-6W
1.3 电路的基本元件(P8)
![]()
![]()
![]()
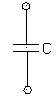
![]()

1.3.1 电阻元件(P8)
| A+ u=3V-----→ i=1.5A-----→ |
u=R·i 电导 G=1/R(西门子 S)
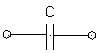
1.3.2 电容元件(P9)
A+ -B -B
u-----→ i-----→ |
电荷 q=C·u
电容(C):C=q/u(法拉 F,微法 μF)
i=dq/dt=dC·u/dt=C·du/dt
1.3.3 电感元件(P11)
| A+ u-----→ i-----→ |
电感(L):亨利(H)微亨(μH)
u=L·di/dt
1.3.4 电压源(P12)
Us=某恒定值,外电路电阻变化时,输出电压不变。
1.3.5 电流源(P13)
Is=某恒定值,外电路电阻变化时,输出电流不变。
1.3.6 受控源(P15)
| 受控源 | 控制支路 | 受控支路 |
| 电压控制电压源(VCVS) | u1 | u2=μu1 |
| 电流控制电压源(ICVS) | i1 | u2=γi1 |
| 电压控制电流源(VCIS) | u1 | i2=gu1 |
| 电流控制电流源(ICIS) | i1 | i2=αi1 |
1.4 基尔霍夫定律
1.4.1 基尔霍夫电流定律(KCL)(P16)
流入节点的电流代数和为零,即 Σi=0
例 1.4.1 流入 a 节点:i1,i2,i3,流出 a 节点:i4,i5
i1+i2+i3-i4-i5=0
1.4.2 基尔霍夫电压定律(KVL)(P17)
回路上电压降的代数和为零,即 Σu=0
1.5.1 二端网络的等效概念(P19)
直流电压源与电流源的等效变换
图 1.5.1(a)电路:u=-iRs+us
图 1.5.1(b)电路:i=is-u/Rs' u=-iRs'+isRs'
比较得到:Rs'=Rs us=isRs'
1.5.2 简单电阻电路的等效变换计算方法(P21)
图 1.5.5 电流源并联合并:is=i1+i2-i3
图 1.5.6 电压源串联合并:us=u1+u2-u3
图 1.5.7(a) 电阻串联分压:u2=us(R2/(R1+R2))
图 1.5.7(b) 电阻并联分流:i2=is(R1/(R1+R2))
图 1.5.9 电阻串联分压:uab=90×(50/(50+10+30))=50V
电位 Uc=Uco=-Uoc=-30V
1.5.3 戴维南定理(P27)
戴维南定理:二端网络等效为电压源 Uoc和电阻 Ro 串联。
Uoc = 二端网络的开路电压,
Ro = 网络中电压源及电流源都为零时的等效电阻。
例 1.5.8 图 1.5.13
I=(20+10)/(0.4+3)=8.82A
Uoc=8.82×3-10=16.5V
Ro=0.4//3=0.353Ω
I3=16.5/(0.353+2)=7.0A
1.5.4 叠加定理(P28)
叠加定理:支路的电压或电流是各电源单独作用时产生的和。
例 1.5.10 图 1.5.14(a) 电路
分别求出电压、电流源单独作用时,
在电阻 6Ω上产生电压降,然后叠加。
1.6 简单的 RC 电路的过渡过程(P29)
RC 电路的充电、放电过渡过程时,
电容电压 uc(t)=uc(∞)+[uc(0)-uc(∞)]e(-1/RC)
初值uc(0)、终值uc(∞)、时间常数τ=RC,
3τ至5τ电路由暂态过渡到稳态。

![]()



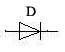
2.1 半导体二极管

4.PN 结的单向导电性(P41)
PN 结的伏安特性(P42)
2.1.2 二极管符号及其主要参数(P43)
最大正向电流 IF、反向击穿电压、最大工作频率 fT。
2.1.3 二极管的应用举例(P44)
例 2.1.1 限幅电路
整流二极管在 100 kHz 失去单向导电性。
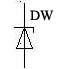
2.1.4 稳压管及其应用(P45)

例 2.1.3 稳压管的稳压值、稳压电流、极限电流Izm。(P46)
| U1(12V) | ----- | ----Uo | |
|
5.6V |
 |
Rmin=(12-5.6)/(82*0.001)=78Ω
选 R=82Ω,则 I1max=(12-5.6)/82=78mA
ILmax=78-5=73mA, RLmix=5.6/0.073=77Ω
2.2 半导体三极管(P46)


2.2.1 三极管的符号及其特性曲线(P47)
共发射极三极管电路及其输出特性曲线:
1.电流放大作用 Ic=βIb。
2.饱和区、放大区、截止区。
2.2.2 三极管的主要参数及其应用举例(P50)
共发射极电流放大系数 β
击穿电压 Uceo
集电极最大电流 Icm
集电极-发射极饱和压降 Uces
例 2.2.1 u1 = 5V,β=125,
三极管饱和时 ube=0.7V,Uces=0.25V。
|
|
Uc 12V |
||
| u1(5V) | 210kΩ |

|
ib=URb/Rb=(u1-ube)/Rb=(5-0.7)/210k=20μA,
三极管饱和时 Uce=Uces=0.25V,
Ic=URc/Rc=(Uc-Uces)/Rc=(12-0.25)/10=1.2 mA
2.2.3 三极管的开关时间和极间电容(P53)
1.开启时间(ton):
延迟时间(td)0—0.1 Icm,上升时间(tr)0.1—0.9 Icm
2.关闭时间(toff):
存储时间(ts)1—0.9 Icm,下降时间(tf)0.9—0.1 Icm
2.2.4 三极管的共基极和共集电极电路(P54)
2.3 MOS 场效应管 (P55)
2.3.1 MOS 管的分类
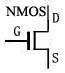
NMOS 管:N 沟道场效应管,ugs,uds 工作电压为正。

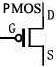
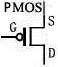
PMOS 管:P 沟道场效应管,ugs,uds 工作电压为负。

2.3.2 增强型 MOS 管的特性曲线(P57)
NMOS 管:压控电流源器件。栅极 G、漏极 D、源极 S。
1.转移特性曲线
开启电压:约 2.0 V
2.输出特性曲线:夹断区、可变电阻区、恒流区。
| U1(0-6V) |  |
UD(0-10V) |
2.3.3 MOS 场效应管的主要参数和应用举例(P58)
输入电阻 rGS 约为 109—1010。
跨导gm = (ΔID/ΔUGS)|UDS=常数
例 2.3.1 NMOS 场效应管构成的反相器。
=10kΩ
输出电压 UO = uDS = uD-iDR1=UD-gmuGSR1
|
|
UD 12V |
|
| u1(5V) |  UO UO |
3.1.1 数制(P66)
二进制(0,1),十六进制(0~9,ABCDEF)
| 十进制 | 二进制 | 八进制 | 十六进制 |
| 0000 | |||
|
|
0001 |
|
|
| |
0010 | |
|
|
|
0011 |
|
|
| |
0100 | |
|
| |
0101 | |
|
|
|
0110 |
|
|
| |
0111 | |
|
|
|
1000 |
|
|
| |
1001 |
|
|
|
|
1010 |
|
A |
|
|
1011 |
|
B |
|
|
1100 |
|
C |
|
|
1101 |
|
D |
|
|
1110 |
|
E |
|
|
1111 |
|
F |
二进、八进、十六进>十进:按位权展开。
例如:
(123)10=(1×100+2×10+3×1)10
(1011)2=(1×8+0×4+1×2+1×1)10=(11)10
(AB9)16=(10×256+11×16+9×1)10=
二进制转换成十六进制:4位二进数 转换成 1位十六进数。
例如:(1101 1011.11)2=(1101 1011.1100B=DB.C)16
十六进制转换成二进制:1位十六进数 转换成 4位二进数。
例如:(123ABC)16=(0001 0010 0011 1010 1011 1100)2
3.1.2 十进制数向二进制数的转换(P68)
例1:138.375转二进制
整数除基取余
138/2=69……0 最低位
69/2=34……1
………………
1/2= 0……1 最高位
小数乘基取整
0.375*2=0.75 余0.75 取整数0 最高位
0.75*2=1.5 余0.5 取整数1
0.5*2=1 余0 取整数1 最低位
138.375转二进制得1000 1010.011
3.1.3 二-十进制码(P69)
| 十进制 | 8421BCD码 |
| 0000 | |
|
|
0001 |
| |
0010 |
|
|
0011 |
| |
0100 |
| |
0101 |
|
|
0110 |
| |
0111 |
|
|
1000 |
| |
1001 |
3.1.4 有符号的二进制数(P70)
1.反码和补码
101100 的反码是 010011
101100 的补码是 010011+1=010100
2.二进制正、负数的表示法
| 十进制 | 原码 | 反码 | 补码 |
| -4 | 1100 | 1011 | 1100 |
| 4 | 0100 | 0100 | 0100 |
3.带符号位的二进制数的补码运算(P71)
| 十进制加法 | 补码加法 |
| -6 +9 |
1111010
0001001 |
| +3 | 10000011 |
3.2 逻辑变量和逻辑代数的三种基本运算(P73)
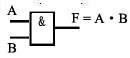
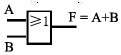
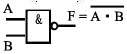
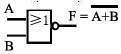
![]()
![]()
![]()
3.2.2 基本的逻辑运算(P73)
1.逻辑加(或运算 OR)
F = A+B 有1出1,全0出0。
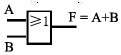
或门符号中的“≥ 1”表示输入1的个数 ≥ 1,输出为1。
2.逻辑乘(与运算 AND)
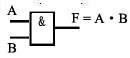
F = A · B 有0出0,全1出1。
3.逻辑反(非运算 NOT)
F = A 入0出1,入1出0。
3.3. 常见的逻辑门电路(P76)
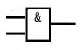
3.3.1 与非门 NAND
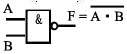
F = A · B 有0出1,全1出0。
3.3.2 或非门 NOR
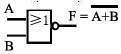
F = A + B 有1出0,全0出1。
3.3.3 与或非门 AOI
F = (A · B)+(C · D)
3.3.4 异或门 exclusive-OR
F = A B + A B 同值出0,异值出1。
异或门符号中的“= 1”表示输入1的个数 = 1,输出为1。
3.3.5 异或非门 exclusive-NOR
F = A B + AB = A⊙B 同值出1,异值出0。
异或非门符号中的“=”表示输入值相等,输出为1。
3.4 逻辑代数的基本定律和规则
3.4.1 基本定律(P80)
1)交换律
2)结合律
3)分配律
A + (B·C) = (A + B)·( A + C) (加对乘分配)
4)吸收律
A +A·B = A (用 B=0,1验证)
A·(A + B) = A
5)0 - 1 律
A + 1 = 1 A + 0 = A
6)互补律
A + A = 1
A · A = 0
7)重叠律
A + A = A
A · A = A
8)对合律
A 的反= A
9)反演律
A + B = A · B (或非 = 非与,)
A · B = A + B (与非 = 非或)
3.4.2 基本规则(P81)
1.代入规则
2.反演规则
“+”“·”互换,“0”“1”互换,“A”“A”互换。
例 3.4.3
F = A·B + C·D
F = (A + B)·(C + D)
3.对偶规则
“+”“ ·”互换,“0”“1”互换。
例 3.4.5
F = A·B + C·D
对偶式 F'= (A + B)·(C + D)
如果 F = L,则对偶式 F'= L'
3.5 常用公式(P82)
1)A·B + A·B = A
证:A·B + A·B = A·(B + B) = A
对偶式:(A + B)·(A + B) = A
2)A + A·B = A + B
证:(A + A)·(A + B) = A + B
对偶式:A·(A + B) = A·B
3)A·B + A·C + B·C = A·B + A·C (包含 B·C)
证:A·B + A·C + B·C = A·B + A·C + (A + A)·B·C
= (A·B + A·B·C) + (A·C + A· B·C) = A·B + A·C
4)(A·B + A·B) 取反= A·B + A·B
(P78 异或的非 = 异或非)
(A·B + A·B) 取反 = A·B + A·B
(P78 异或非的非 = 异或)
3.6 逻辑函数的标准形式
3.6.1 由真值表写出逻辑表达式(P83)
例 3.6.1 F = ABC + ABC + AB C + ABC
| 十进制 | m | 最小项 | 输入 | 输出
F |
||
| A | B | C | ||||
| m0 | A B C | 0 | 0 | 0 | 0 | |
|
|
m1 | A BC | 0 | 0 | 1 | 0 |
| |
m2 | ABC | 0 | 1 | 0 | 1 |
|
|
m3 | ABC | 0 | 1 | 1 | 1 |
| |
m4 | AB C | 1 | 0 | 0 | 1 |
| |
m5 | ABC | 1 | 0 | 1 | 0 |
|
|
m6 | ABC | 1 | 1 | 0 | 0 |
| |
m7 | ABC | 1 | 1 | 1 | 1 |
例 3.6.2 含 1 个数的奇偶校验
| 十进制 | m | 最小项 | 输入 | 输出
F |
|||
| A | B | C | D | ||||
| m0 | A B C D | 0 | 0 | 0 | 0 | 0 | |
|
|
m1 | A B CD | 0 | 0 | 0 | 1 | 1 |
| |
m2 | A BCD | 0 | 0 | 1 | 0 | 1 |
|
|
m3 | A BCD | 0 | 0 | 1 | 1 | 0 |
| |
m4 | ABC D | 0 | 1 | 0 | 0 | 1 |
| |
m5 | ABCD | 0 | 1 | 0 | 1 | 0 |
|
|
m6 | ABCD | 0 | 1 | 1 | 0 | 0 |
| |
m7 | ABCD | 0 | 1 | 1 | 1 | 1 |
|
|
m8 | AB C D | 1 | 0 | 0 | 0 | 1 |
| |
m9 | AB CD | 1 | 0 | 0 | 1 | 0 |
|
|
m10 | ABCD | 1 | 0 | 1 | 0 | 0 |
|
|
m11 | ABCD | 1 | 0 | 1 | 1 | 1 |
|
|
m12 | ABC D | 1 | 1 | 0 | 0 | 0 |
|
|
m13 | ABCD | 1 | 1 | 0 | 1 | 1 |
|
|
m14 | ABCD | 1 | 1 | 1 | 0 | 1 |
|
|
m15 | ABCD | 1 | 1 | 1 | 1 | 0 |
3.6.2 最小项(P85)
最小项:每个变量以原变量或反变量出现一次。
例 3.6.1 F(A,B,C)
= ABC + ABC + AB C + ABC
= m2 + m3 + m4 + m7
= Σm(2,3,4,7)
3.7 逻辑函数的代数化简方法(P87)
F(A,B,C) = AB + BC + AB C
逻辑表达式的与-或关系,应减少与项和变量个数,
简化与门、或门组成的实现电路。

![]()
![]()
![]()
| A B |
 |
|
| B C |
 |
|
| A B C |
 |
1)合并法
例 3.7.1 ABC + AB C = AB
4)消项法
利用包含律 A B + A C + B C = A B + A C
3.8 逻辑函数的卡诺图化简法(P89)
相邻行列只改变一个输入变量。
二变量卡诺图
| B | |||
| A | 0 | 1 | |
| 2 | 3 | ||
三变量卡诺图
| BC | |||||
| A | 0 | 1 | 3 | 2 | |
| 4 | 5 | 7 | 6 | ||
四变量卡诺图
| CD | |||||
| AB | 0 | 1 | 3 | 2 | |
| 4 | 5 | 7 | 6 | ||
| 12 | 13 | 15 | 14 | ||
| 8 | 9 | 11 | 10 | ||
3.8.2 利用卡诺图进行逻辑化简(P90)
最小项编号,如 ABCD = 0010 为 2号。
| BA | |||||
| DC | 0 | 8 | 12 | 4 | |
| 2 | 10 | 14 | 6 | ||
| 3 | 11 | 15 | 7 | ||
| 1 | 9 | 13 | 5 | ||
输出为 1 的方格,由方格群写出表达式。
F = A B + ABC
| BA | |||||
| DC | 1 | 0 | 0 | 0 | |
| 1 | 0 | 1 | 0 | ||
| 1 | 0 | 1 | 0 | ||
| 1 | 0 | 0 | 0 | ||
3.8.3 随意项(P92)
约束方程 Σd(10,11,12,13,14,15)= 0
显示七段显示译码器中的 a 字段。
| a | ||
| f
e |
 |
b
c |
| d |
| 十进制 | m | 输入 | 输出
Fa |
|||
| A3 | A2 | A1 | A0 | |||
| m0 | 0 | 0 | 0 | 0 | 1 | |
|
|
m1 | 0 | 0 | 0 | 1 | 0 |
| |
m2 | 0 | 0 | 1 | 0 | 1 |
|
|
m3 | 0 | 0 | 1 | 1 | 1 |
| |
m4 | 0 | 1 | 0 | 0 | 0 |
| |
m5 | 0 | 1 | 0 | 1 | 1 |
|
|
m6 | 0 | 1 | 1 | 0 | 1 |
| |
m7 | 0 | 1 | 1 | 1 | 1 |
|
|
m8 | 1 | 0 | 0 | 0 | 1 |
| |
m9 | 1 | 0 | 0 | 1 | 1 |
|
|
m10 | 1 | 0 | 1 | 0 | x |
|
|
m11 | 1 | 0 | 1 | 1 | x |
|
|
m12 | 1 | 1 | 0 | 0 | x |
|
|
m13 | 1 | 1 | 0 | 1 | x |
|
|
m14 | 1 | 1 | 1 | 0 | x |
|
|
m15 | 1 | 1 | 1 | 1 | x |
按输出为 1 的方格,由方格群写出表达式。
Fa = A3 + A1 + A2 A0 + A2 A0
按输出为 0 的方格,由方格群写出表达式。
Fa = A2 A1 A0 + A3 A2 A1 A0
| A1A0 | |||||
| A3A2 | 1 | 0 | 1 | 1 | |
| 0 | 1 | 1 | 1 | ||
| x | x | x | x | ||
| 1 | 1 | x | x | ||