高校计算机教材
计算机图形学
2003.7.1.
第一章 绪论
概念:计算机图形学、图形、图像、点阵法、参数法、
图形的几何要素、非几何要素、数字图像处理;
计算机图形学和计算机视觉的概念及三者之间的关系;
计算机图形系统的功能、计算机图形系统的总体结构。
第二章 图形设备
图形输入设备:有哪些。
图形显示设备:CRT的结构、原理和工作方式。
彩色CRT:结构、原理。
随机扫描和光栅扫描的图形显示器的结构和工作原理。
图形显示子系统:分辨率、像素与帧缓存、颜色查找表等基本概念,分辨率的计算
第三章 交互式技术
什么是输入模式的问题,有哪几种输入模式。
第四章 图形的表示与数据结构
自学,建议至少阅读一遍
第五章 基本图形生成算法
概念:点阵字符和矢量字符;
直线和圆的扫描转换算法;
多边形的扫描转换:有效边表算法;
区域填充:4/8连通的边界/泛填充算法;
内外测试:奇偶规则,非零环绕数规则;
反走样:反走样和走样的概念,过取样和区域取样。
5.1.2 中点 Bresenham 算法(P109)
| 斜率 K | 误差项 d | 理想点 Q | 取下一个点 | d 更新 |
| <1 | <0 | 在中点上 | 取上点 | d+2△x-2△y |
| >=0 | 在中点下 | 取下点 | d-2△y | |
| >1 | <0 | 在中点右 | 取右点 | d-2△x+2△y |
| >=0 | 在中点左 | 取左点 | d-2△x | |
| <-1 | <0 | 在中点左 | 取左点 | d-2△x+2△y |
| >=0 | 在中点右 | 取右点 | d-2△x | |
| >-1 | <0 | 在中点下 | 取下点 | d+2△x-2△y |
| >=0 | 在中点上 | 取上点 | d-2△y |
5.1.2 改进 Bresenham 算法(P112)
| 斜率 K | 改进误差项 e | 理想点 Q | 取下一个点 | e 更新 |
| <1 | <0 | 在中点上 | 取上点 | e-2△x |
| >=0 | 在中点下 | 取下点 | e+2△y | |
| >1 | <0 | 在中点右 | 取右点 | e-2△y |
| >=0 | 在中点左 | 取左点 | e+2△x | |
| <-1 | <0 | 在中点左 | 取左点 | e-2△y |
| >=0 | 在中点右 | 取右点 | e+2△x | |
| >-1 | <0 | 在中点下 | 取下点 | e-2△x |
| >=0 | 在中点上 | 取上点 | e+2△y |
习题5 (P144)
5.3 试用中点Bresenham算法画直线段的原理推导斜率为负且大于1的直线段绘制过程
(要求写清原理、误差函数、递推公式及最终画图过程)。(P111)
解: k<=-1 |△y|/|△x|>=1 y为最大位移方向
故有 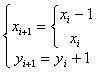
构造判别式: ![]()
推导d各种情况的方法(设理想直线与y=yi+1的交点为Q):
所以有: yQ-kxQ-b=0 且 yM=yQ
d=f(xM-kxM-b-(yQ-kxQ-b)=k(xQ-xM)
所以,当k<0,
d>0时,M点在Q点右侧(Q在M左),取左点 Pl(xi-1,yi+1)。
d<0时,M点在Q点左侧(Q在M右),取右点 Pr(xi,yi+1)。
d=0时,M点与Q点重合(Q在M点),约定取右点 Pr(xi,yi+1) 。
所以有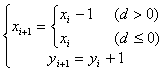
递推公式的推导:
d2=f(xi-1.5,yi+2)
当d>0时,
d2=yi+2-k(xi-1.5)-b 增量为1+k
=d1+1+k
当d<0时,
d2=yi+2-k(xi-0.5)-b 增量为1
=d1+1
当d=0时,
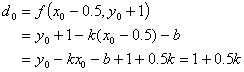
5.7 利用中点 Bresenham 画圆算法的原理,
推导第一象限y=0到y=x圆弧段的扫描转换算法
(要求写清原理、误差函数、递推公式及最终画图过程)。(P115)
| y坐标 | 圆心角 α | 误差项 d | 理想点 Q | 取下一个点 | d 更新 |
| y=0 y=x |
0°<=α<=45° | <0 | 在中点右 | 取右点 | d+2y+3 |
| >=0 | 在中点左 | 取左点 | d-2(y-x)+5 | ||
| y=x y=1 |
45°<=α<=90° | <0 | 在中点上 | 取上点 | d+2x+3 |
| >=0 | 在中点下 | 取下点 | d-2(x-y)+5 |
解:在x=y到y=0的圆弧中,(R,0)点比在圆弧上,算法从该点开始。
最大位移方向为y,由(R,0)点开始,y渐增,x渐减,每次y方向加1,x方向减1或减0。
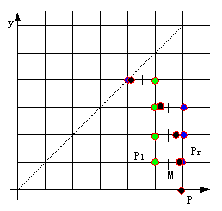
设P点坐标(xi,yi),下一个候选点为右点Pr(xi,yi+1)和左点Pl(xi-1,yi+1),
取Pl和Pr的中点M(xi-0.5,yi+1),设理想圆与y=yi+1的交点Q,
构造判别式:
d=f(xM,yM)=(x-0.5)2+(yi+1)2+R2
当d<0时,M在Q点左方(Q在M右),取右点Pr(xi,yi+1)
当d>0时,M在Q点右方(Q在M左),取左点Pl(xi-1,yi+1)
当d=0时,M与Q点重合,约定取左点Pl(xi-1,yi+1)
所以有: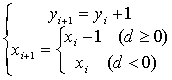
推导判别式:
d>=0时,取左点Pl(xi-1,yi+1),下一点为(xi-1,yi+2)和(xi-2,yi+2)
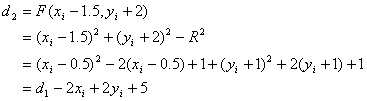
d<0时,取右点Pr(xi,yi+1),下一点为(xi,yi+2)和(xi-1,yi+2)
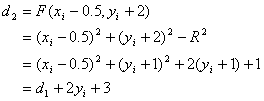
d0=f(R-0.,1)=R2-R+0.25+1-R2=1.25-R
5.11 如图5-59所示多边形,若采用扫描转换算法(ET边表算法)进行填充,
试写出该多边形的边表ET和当扫描线Y=4时的有效边表AET(活性边表)。(P125)
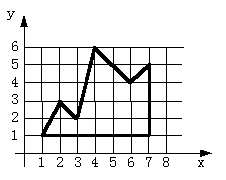
解:
1)边表ET表
|
x|ymin |
ymax | 1/k | next |
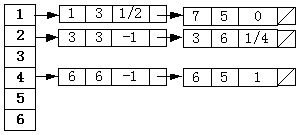
2)y=4时的有效边表AET
|
x |
ymax | 1/k | next |

注意:水平线不用计算。
5.22 构造两个例子,一个是4-连通图,其边界是8-连通的,
另一个是8-连通图,其边界是4-连通的。(P132)
解:
4-连通区域 8-连通区域
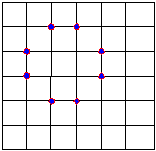
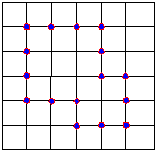
第六章 二维变换及二维观察
概念:齐次坐标,窗口,视区,二维观察流程,
字符裁减的三种策略,外部裁减
计算:二维几何变换
直线裁减:区域编码法和梁友栋算法
多边形裁减:逐边裁减法和双边裁减法
6.1.3 二维变换矩阵(P147)
| 3阶二维变换矩阵 | 子矩阵功能 |
| a b p
c d q l m s |
abcd 比例旋转 pq
投影变换
lm 平移变换 s 整体比例 |
6.2.3 旋转变换(P149)
| 逆时针变换矩阵 | 顺时针变换矩阵 |
| cosθ sinθ
0
-sinθ cosθ 0 0 0 1 |
cosθ -sinθ
0
sinθ cosθ 0 0 0 1 |
6.2.5 相对任一参考点的二维几何变换(P155)
例如:相对(xf,yf)点的旋转变换
| 平移到 坐标原点 |
旋转角度θ | 反平移回 原来位置 |
| 1 0 0
0 1 0 -xf -yf 1 |
cosθ sinθ 0
-sinθ cosθ 0 0 0 1 |
1 0
0
0 1 0 xf yf 1 |
习题6 (P177)
6.7 求四边形 ABCD 绕 P(5,4)旋转45度的变换矩阵和端点坐标,
画出变换后的图形。(P147 P148 P155)
解:变换的过程包括:
1)平移:将点P(5,4)平移至原点(0,0),
2)旋转:图形绕原点(0点)旋转45度,
3)反平移:将P点移回原处(5,4),
4)变换矩阵:平移—旋转—反平移
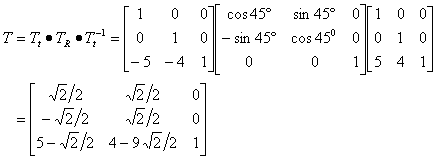
5)变换过程:四边形 ABCD 的规范化齐次坐标(x,y,1) * 3阶二维变换矩阵
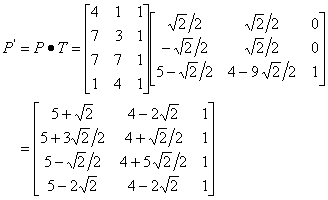
由旋转后四边形 ABCD 的规范化齐次坐标(x',y',1)可写出顶点坐标:
A'(6.4,1.2) B'(7.1,4.7) C'(4.3,8.5) D'(2.2,1.2)
6.15 用梁友栋算法裁减线段AB,B点的坐标改为(-2,-1)(P170)
解:以A(3,3)为起点,B(-2,-1)为终点
所以有x1=3,y1=3,x2=-2,y2=-1,wxl=0,wxr=2,wyb=0,wyt=2
构造直线参数方程:
|
x=x1+u(x2-x1) |
|||
| 0 | x1 | x | x2 |
| y |
A(3,3) |
|||||
| 3 | C(7 |
/4,2) |
||||
| 2 |
|
|||||
| D( |
0,3/ |
5) 1 | ||||
| -2 | -1 | 0 | 1 | 2 | 3 | x |
| B(-2,-1) | -1 | |||||
x=x1+u(x2-x1) (0<=u<=1)
y=y1+u(y2-y1)
把 x1=3,y1=3,x2=-2,y2=-1 代入得
x=3-5u
y=3-4u
计算各个p和q值有:
p1=x1-x2=5 q1=x1-wxl=3
p2=x2-x1=-5 q2=wxr-x1=-1
p3=y1-y2=4 q3=y1-wyb=3
p4=y2-y1=-4 q4=wyt-y1=-1
根据,uk=qk/pk 算出
pk<0时:u2=1/5 u4=1/4
pk>0时:u1=3/5 u3=3/4
umax=MAX(0,u2,u4)=MAX(0,1/5,1/4)=1/4 (取最大值)
umin=MIN(u1,u3,1)=MIN(3/5,3/4,1)=3/5 (取最小值)
由于 umax<umin ,故此直线AB有一部分在裁减窗口内,
pk<0时,将 umax=1/4 代入直线参数方程
x=x1+u(x2-x1)
x=3+1/4*(-5)=3-5/4=7/4
y=y1+u(y2-y1)
y=3+1/4*(-4)=2
求出直线在窗口内部分的端点C(7/4,2)
pk>0时,将 umin=3/5 代入直线参数方程
x=x1+u(x2-x1)
x=3+3/5*(-5)=0
y=y1+u(y2-y1)
y=3+3/5*(-4)=3/5
求出直线在窗口内部分的端点D(0,3/5)。
所以,直线在窗口内部分的端点为C(7/4,2),D(0,3/5)。
第七章 三维变换及三维观察
概念:几何变换、投影变换、透视投影、平行投影、灭点
平面几何投影的分类以及分类原则
计算:三维几何变换、三视图
7.2 三维几何变换(P180)
| 4阶三维变换矩阵 | 子矩阵功能 |
| a b c p
d e f q g h i r l m n s |
abcdefghi 比例旋转 pqr 透视投影
lmn 平移变换 s 整体比例 |
整体比例变换(P182)
s>1 时,整体缩小,如 2 表示2:1缩小。
s<1 时,整体放大,如 1/2 表示1:2放大。
7.3.1 正投影
1.主视图 V(P191)
4阶三维变换矩阵
| y 轴方向投影 |
| 1 0
0 0
0 0 0 0 0 0 1 0 0 0 0 1 |
2.俯视图 H
| 4阶三维变换矩阵 |
| 1 0
0 0
0 0 -1 0 0 0 0 0 0 0 -z0 1 |
| z 轴方向投影 | 绕 x 轴旋转-90度 | z 轴方向平移-1 |
| 1 0 0
0
0 1 0 0 0 0 0 0 0 0 0 1 |
1
0
0
0
0 cos(-90°) sin(-90°) 0 0 -sin(-90°) cos(-90°)0 0 0 0 1 |
1 0
0 0
0 1 0 0 0 0 1 0 0 0 -z0 1 |
3.侧视图 W(P192)
| 4阶三维变换矩阵 |
| 0
0 0 0
-1 0 0 0 0 0 1 0 -x0 0 0 1 |
| x 轴方向投影 | 绕 z 轴旋转90度 | x 轴方向平移-1 |
| 0
0 0 0
0 1 0 0 0 0 1 0 0 0 0 1 |
0 cos90° sin90° 0
0 -sin90° cos90° 0 0 0 1 0 0 0 0 1 |
1
0 0 0
0 1 0 0 0 0 1 0 -x0 0 0 1 |
习题7 (P213)
7.5 求空间四面体关于点 P(2,-2,2)整体放大2倍的变换矩阵,
画出变换后的图形。(P182)
解:关于点 P(2,-2,2)整体放大两倍,
变换矩阵:点 P(2,-2,2)平移至原点--比例变换放大两倍--反平移回点 P(2,-2,2)。
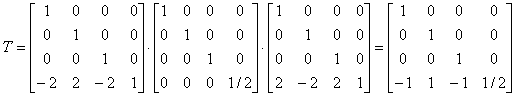
变换过程:空间四面体 ABCD 的规范化齐次坐标(x,y,z,1) * 4阶三维比例变换矩阵

空间四面体 ABCD 的齐次坐标(x',y',z',1/2)转换成规范化齐次坐标
| 顶点 |
x y z 1 |
| A
B C D |
2,2,-2,1
2,6,-2,1 -2,6,-2,1 2,6, 2,1 |
由比例变换后规范化齐次坐标(x',y',z',1)可写出顶点坐标:
A'(2,2,-2) B'(2,6,-2) C'(-2,6,-2) D'(2,6,2)
7.7 求空间四面体 ABCD 三视图的变换矩阵(平移矢量均为1),并作出三视图。(P180)
解:
1)主视图V(P191)
空间四面体 ABCD 的规范化齐次坐标矩阵 * Y轴方向投影矩阵(不需要平移)
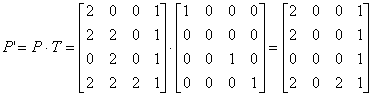
2)俯视图H(P191)
Z轴方向投影矩阵 * 绕X轴旋转-90度矩阵 * Z轴方向平移-1矩阵
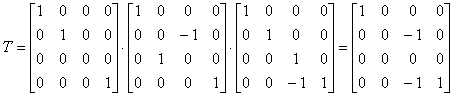
空间四面体 ABCD 的规范化齐次坐标矩阵 * 投影变换矩阵(可以直接写出)
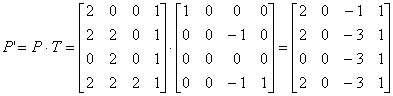
3)侧视图W(P192)
X轴方向投影矩阵 * 绕Z轴旋转90度矩阵 * X轴方向平移-1矩阵

空间四面体 ABCD 的规范化齐次坐标矩阵 * 投影变换矩阵(可以直接写出)
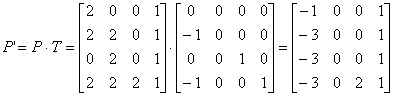
4)画图注意:三个图画在同一坐标系中,点与点的连接关系以及直线的可见性问题。
华中科技大学网络学院
2002-2003学年度第一学期
《计算机图形学》考试试题
一、填空
2.帧缓存(P42):(1024*768*8/8)/1024=768kB
颜色位面数(P43):24
总颜色数:(2^8)^3=2^24=(2^4)*(2^20)=16MB
二、名词解释
三、简答与计算
3.边标志算法(P128)
解:打标记:x1,x2,x3,x4
填充:x1与x2,x3与x4扫描线区间的像素点。
5.正则集合运算(P88)
解:通常意义下的集合求交运算:C=A∩B 有一条弧立边
正则集合运算:C=A∩*B 无弧立边
四、计算作图题
1.中点 Bresenham 算法(P109)
| 斜率 K | 误差项 d | 理想点 Q | 取下一个点 | d 更新 |
| <1 | <0 | 在中点上 | 取上点 | d+2△x-2△y |
| >=0 | 在中点下 | 取下点 | d-2△y |
解:直线斜率:k=(6-1)/(9-1)=5/8 0<k<1
计算初值:△x=9-1=8 △y=6-1=5 d=△x-2△y=8-2*5=-2
取上点:2△x-2△y=2*8-2*5=6 d+2△x-2△y=-2+6=4
取下点:2△y=2*5=10 d-2△y=4-10=-6
| x | y | 误差项 d | 取下一个点 | d 更新 |
| 1 | 1 | <0 | 取上点 | d+2△x-2△y=4 |
| 2 | 2 | >0 | 取下点 | d-2△y=-6 |
| 3 | 2 | <0 | 取上点 | d+2△x-2△y=0 |
| 4 | 3 | =0 | 取下点 | d-2△y=-10 |
| 5 | 3 | <0 | 取上点 | d+2△x-2△y=-4 |
| 6 | 4 | <0 | 取上点 | d+2△x-2△y=2 |
| 7 | 5 | >0 | 取下点 | d-2△y=-8 |
| 8 | 5 | <0 | 取上点 | d+2△x-2△y=-2 |
| 9 | 6 |
2.改进的有效边表算法(P125)
解:1)边表 ET:交点x(最小y坐标 ymin)
|
x|ymin |
ymax | 1/k | next |
| x坐标 | ||||||||||
| 1 | CB边 | CA边 | ||||||||
| 2 | → | 6 | 5 | -4/3 | → | 6 | 9 | -2/7 | / | |
| 3 | ||||||||||
| 4 | BA边 | |||||||||
| 5 | → | 2 | 9 | -1/2 | / | |||||
| 6 7 8 9 |
||||||||||
2)y=4的有效边表 AET:交点x
|
x |
ymax | 1/k | next |
| y=4 | ||||||
| | | 与CB边相交 | |||||
| ┗ | → | 3.3 | 5 | -4/3 | ┓ | |
| ┏ | ————————— | ┛ | ||||
| | | 与CA边相交 | |||||
| ┗ | → | 5.4 | 9 | -1/2 | / | |
3)y=4时的填充交点对:(3.3,4) (5.4,4)
3.求三角形绕B点(2,5)旋转 θ 的变换矩阵。
求三角形绕B点顺时针旋转90度后各端点坐标。(P125)
解:1)三角形绕B点(2,5)旋转 θ 的变换矩阵
T=Tt * TR * Tt-1
| 平移到 坐标原点 |
旋转角度θ | 反平移回 原来位置 |
| 1 0 0
0 1 0 -2 -5 1 |
cosθ sinθ 0
-sinθ cosθ 0 0 0 1 |
1 0 0
0 1 0 2 5 1 |
2)三角形绕B点顺时针旋转90度的变换矩阵,θ=-90°
T=Tt * TR * Tt-1
| 平移到 坐标原点 |
旋转角度θ | 反平移回 原来位置 |
| 1 0 0
0 1 0 -2 -5 1 |
cos90° -sin90°
0
sin90° cos90° 0 0 0 1 |
1 0 0
0 1 0 2 5 1 |
变换过程:三角形 ABC 的规范化齐次坐标(x,y,1) * 3阶二维变换矩阵
P=P * T
得到三角形 ABC 变换后的规范化齐次坐标(x',y',1)
| 顶点 |
x y 1 |
| A
B C |
4.6
2 1
2 5 1 0 -1 1 |
可以写出顶点坐标:A'(4.6,2) B'(2,5) C'(0,-1)
4.用编码裁剪算法裁剪线段P1(0,2)P2(3,3)。要求写出:(164)
1)窗口边界划分的9个区间的编码原则;
2)线段端点的编码;
3)裁剪的主要步骤;
4)裁剪的输出结果。
解:线段P1(0,2)P2(3,3)的编码裁剪
| y | 1001 | 1000 | 1010 | ||
| 4 |
0001 |
P2(3,3)
0000 S
|
0010 |
||
| 3 | |||||
| P1(0,2) 2 | |||||
| 1 |
0101 |
0100 | 0110 | ||
| 0 | 1 | 2 | 3 | 4 | x |
1)窗口边界划分的9个区间的编码原则;
| 编码 | D3 | D2 | D1 | D0 |
| 窗口外 | 上边top | 下边bottom | 右边right | 左边left |
| 条件 | y>wyt
wyt=4 |
y<wyb
wyb=1 |
x>wxr
wxr=4 |
x<wxl
wxl=1 |
| 取值 | D3=1 | D2=1 | D1=1 | D0=1 |
2)线段端点的编码;
P1 code1=0001, P2 code2=0000
3)裁剪的主要步骤;
输入 P1(0,2), P2(3,3), wyt=4, wyb=1, wxr=4, wxl=1;
P1 code1=0001, P2 code2=0000;
code1|code2≠0 不能简取;code1&code2=0 不能简弃;
求线段 P1(0,2)P2(3,3)和 窗口左界wxl=1 的交点,
把 wxl=1 代入直线方程求出 y=kx+b=(1/3)*x+2=2.3
交点坐标S(1,2.3)替换端点坐标P1(0,2),使P1坐标为(1,2.3);
去掉P1S线段,输出线段P1P2。
4)裁剪的输出结果:P1(1,2.3)P2(3,3)。
5.用改进 Bresenham 算法画直线段的原理,
推导斜率 K>1 的直线段的扫描转换算法。(P112)
| 斜率 K | 改进误差项 e | 理想点 Q | 取下一个点 | e 更新 |
| >1 | <0 | 在中点右 | 取右点 | e-2△y |
| >=0 | 在中点左 | 取左点 | e+2△x |
解: k>1 y为最大位移方向
故有
| yi+1= | yi+1 |
| xi+1= | xi+1 (d>0.5 取右点Pr) |
| xi (d<=0.5 取左点Pl) |
误差项 d 的初值为0 d=d+1/k
当 x 方向走一步 d-1
令 e=d-0.5
| yi+1= | yi+1 |
| xi+1= | xi+1 (e>0 取右点Pr) |
| xi (e<=0 取左点Pl) |
改进误差项 e 的初值为 e=d-0.5=0-0.5=-0.5;
避免计算小数和除法,改进误差项 e 用2e△y。
算法步骤:
1)输入:Po(xo,yo) P1(x1,y1);
2)计算初值:△x,△y, e=2e△y=2*(-0.5)△y=-△y, x=xo, y=yo。
3)画点:P(x,y)
4)改进误差项 e 更新:
| 斜率 K | 改进误差项 e | 理想点 Q | 取下一个点 | e 更新 |
| >1 | <0 | 在中点右 | 取右点 | e-2△y |
| >=0 | 在中点左 | 取左点 | e+2△x |